Samples

Introduction

In this section we show the results of several test calculations obtained from the “skeleton-RHF” and OpenFMO codes. To this end, we used the ACC nodes of System B of Institute for Solid State Physics (ISSP) supercomputer at the University of Tokyo; the configuration of ACC node is as follows:

• CPU: 2 Intel Xeon E5-2680 v3 2.5GHz (12core * 2)
• GPU: 2 nVIDIA Tesla K40 ( 2880 CUDA core * 2)
• MEM: DDR4-2133 128GB
• FDR InfiniBand

The compilers and libraries used are as follows:

• icc version 16.0.4 (gcc version 4.8.5 compatibility)
• mpiicc for the Intel(R) MPI Library 5.1.3 for Linux*
• Cuda compilation tools, release 7.0, V7.0.27

Glycylglycine

We again treat the FMO-RHF/STO-3G calculation of one glycylglycine illustrated in Figure 2, whose input file is explained in Simple Example (Glycylglycine). You can download the input (digly-ofmo-rhf.inp), output (digly-ofmo-rhf.out), and PBS job (job.sh) files used. For the calculation, we used one ACC node with 1 data server of 1 rank and 2 worker groups of 1 rank.

We also performed the RHF/STO-3G calculation with “skeleton-RHF” code on the same glycyglycine. You can download the input (digly-rhf.inp), output (digly-rhf.inp), and PBS job (job2.sh) files used. For the calculation, we performed 24 threads execution of “skeleton-RHF” code with one GPU unit.

We can see the FMO-RHF/STO-3G calculation reproduces the energy of the molecule obtained from the RHF/STO-3G calculation, as listed in Table 11

Table 11. Total SCF Energy (in hartree) of Glycylglycine

RHF	FMO
-483.23779373	-483.23772776

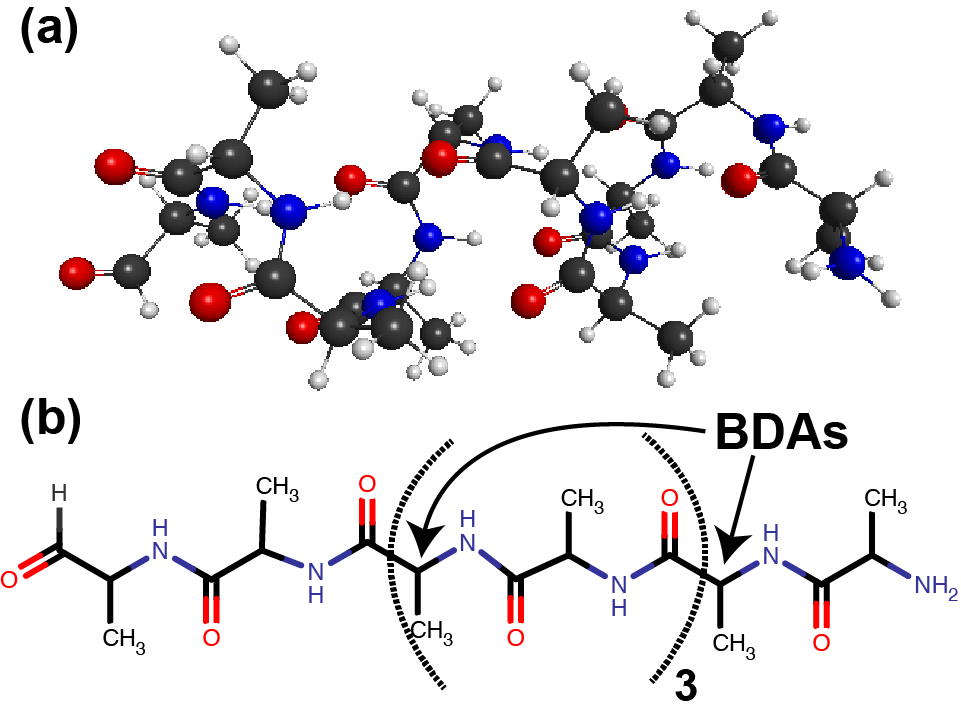
ala10 in alpha-helix conformation

We demonstrate the FMO-RHF/6-31G(d) calculation of the alanine polypeptide in an ideal alpha-helix conformation (called ala10 hereafter) plotted in Figure 3. The alpha-carbon atoms, as marked by the arrows in Figure 3 (b), are treated as bond-detached atoms (BDAs). The coordinate is taken from the previous study [NA11]. The input (ala10-ofmo-rhf.inp), output (ala10-ofmo-rhf.out), and PBS job (job3.sh) files used can be downloaded. For the calculation, we used one ACC node with 1 data server of 1 rank and 2 worker groups of 1 rank.

Figure 3. ala10: (a) Structure (b) Fragmentation

We also performed the RHF/6-31G(d) calculation with “skeleton-RHF” code on the same ala10. You can download the input (ala10-rhf.inp), output (ala10-rhf.out), and PBS job (job4.sh) files used. For the calculation, we performed 24 threads execution of “skeleton-RHF” code with one GPU unit.

Table 12 compares the resultant FMO-RHF/6-31G(d) energy with the RHF/6-31G(d) one. Table 12 also lists the RHF/6-31G(d) and FMO-RHF/6-31G(d) energies of ala10 calculated with GAMESS; you can download the input files ( Ala10AlphaRhfN31d.inp and Ala10AlphaFmoRhfN31d.inp) used for GAMESS.

Table 12. Total SCF Energy (in hartree) of ala10 from OpenFMO and GAMESS

OpenFMO		GAMESS
RHF	FMO	RHF	FMO
-2459.51658600	-2459.51865445	-2459.51658597	-2459.51863956

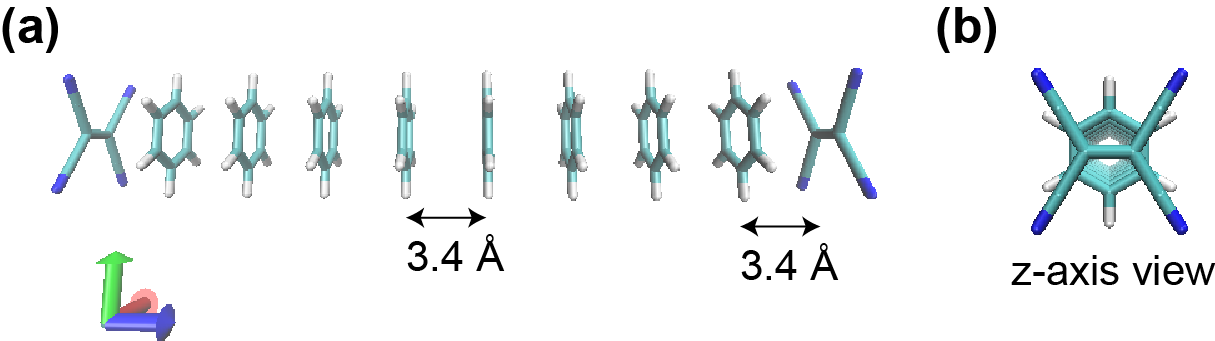
TCNE-(Benzene)8-TCNE

We, here, demonstrate a FMO-RHF/6-31G(d,p) calculation of the model system TCNE-(Benzene)8-TCNE, where eight perfectly eclipsed-stack benzene molecules are sandwiched by tetracyanoethylene (TCNE), as plotted in Figure 4. You can download the input (TcneBenzen8Tcne-ofmo-rhf.inp), output (TcneBenzen8Tcne-ofmo-rhf.out), and PBS job (job5.sh) files. The coordinate is taken from the previous study [NA11]. The FMO calculation treats each isolated molecule as a fragment, thereby involving no bond detachement. Note that the input file for OpenFMO has to define $FMOBND and $FMOLMO/$FMOHYB groups if its FMO calculation involves no bond detachment , as TcneBenzen8Tcne-ofmo-rhf.inp; in that case, the OpenFMO code does NOT use the hybrid molecular orbitals defined by $FMOLMO/$FMOHYB group in the calculation and read the blank line defined by $FMOBND group. See $FMOLMO or $FMOHYB Group and $FMOBND Group. For the calculation, we used 8 ACC nodes with 1 data server of 1 rank and 6 worker groups of 1 rank.

Figure 4. Structure of TCNE-(Benzene)8-TCNE possessing D2h molecular symmetry

In addition, You can download the input (TcneBenzen8Tcne-rhf.inp), output (TcneBenzen8Tcne-rhf.out), and PBS job (job6.sh) files used for the RHF/6-31G(d,p) calculation with “skeleton-RHF” code. Table 13 compares the resultant FMO-RHF/6-31G(d,p) energy with the RHF/6-31G(d,p) one.

Table 13. Total SCF Energy (in hartree) of TCNE-(Benzene)8-TCNE

RHF	FMO
-2735.45391614	-2735.45313547

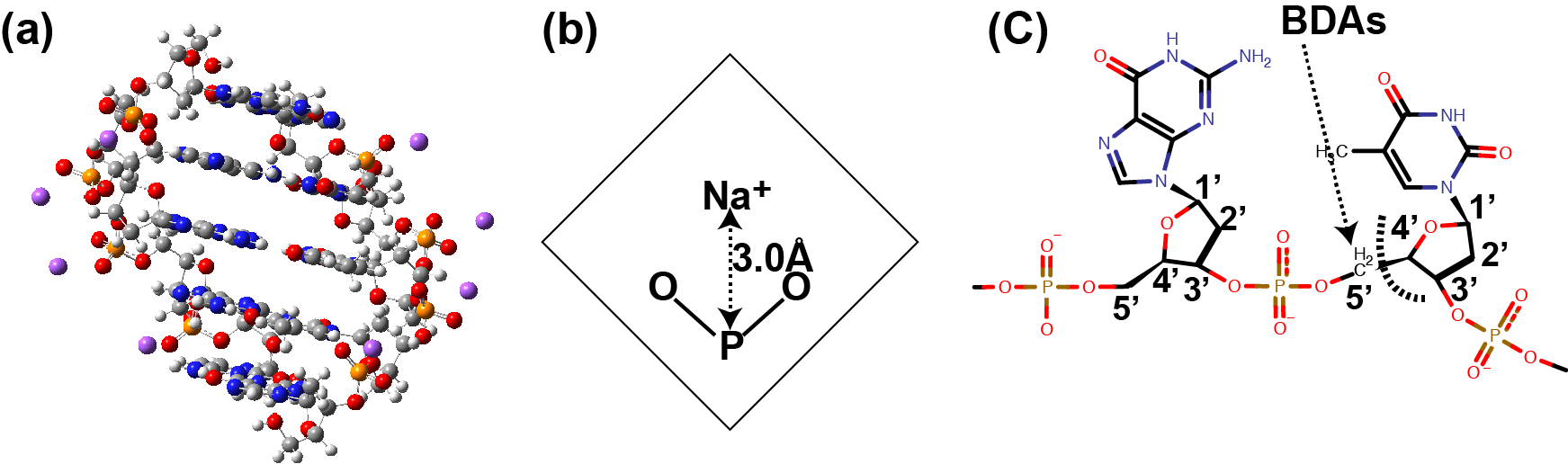
DNA

This subsection shows an example of the FMO-RHF/6-31G(d) calculation of dephosphorilated GTTTG B-DNA oligomer (dGTTTG) neutralized by 8 Na+ ions, as illustrated in Figure 5 (a). You can download the input (dna-ofmo-rhf.inp), output (dna-ofmo-rhf.out), and PBS job (job7.sh) files. We constructed the structure of dGTTTG by using the NBA program from AmberTools package in line with the previous study [RP14]. Figure 5 (b) shows how to place Na+ ion, which follows the previous study [FWK+14]. Figure 5 (c) shows that the FMO calculation treats the cabon atoms at the 5’ and 4’ positions as BDA (bond-detached atom) and BAA (bond-attached atom), respectively. For the calculation, we used 8 ACC nodes with 1 data server of 1 rank and 6 worker groups of 1 rank.

Figure 5. dGTTTG with 8 Na+ ions: (a) Structure, (b) Placement of Na+ ion, and (c) Fragmentation

For comparison, we performed the same calculation using OpenFMO turning off its GPU acceleration; you can see the detail of the results in the output file dna-ofmo-rhf-offgpu.out. Table 14 lists the total SCF energy and computational time obtained using OpenFMO with/without GPU units. Note that the computational times taken from the output files, which are printed as “total etime = …”, are crude, but are probably useful information in this test calculation. We can confirm that the usage of GPU units does NOT affect the resultant SCF energy. The GPU-accelerated OpenFMO halves the computational time calculated with the OpenFMO even though the system size is modest and the computational settings, such as the types of the two-electron integral, are not optimized.

Table 14. Total SCF Energy (in hartree) and Computational Time (seconds) of dGTTTG with 8 Na+ ions obtained from OpenFMO

	SCF Energy	Computational Time
CPU + GPU	-14004.75470797	1049.715826
Only CPU	-14004.75470797	2154.053616

[FWK+14]

Kaori Fukuzawa, Chiduru Watanabe, Ikuo Kurisaki, Naoki Taguchi, Yuji Mochizuki, Tatsuya Nakano, Shigenori Tanaka, and Yuto Komeiji. Accuracy of the fragment molecular orbital (fmo) calculations for dna: total energy, molecular orbital, and inter-fragment interaction energy. Comput. Theor. Chem., 1034:7 – 16, 2014. URL: http://www.sciencedirect.com/science/article/pii/S2210271X14000577, doi:https://doi.org/10.1016/j.comptc.2014.02.002.

[NA11]

(1, 2) Hirotaka Nishioka and Koji Ando. Electronic coupling calculation and pathway analysis of electron transfer reaction using ab initio fragment-based method. i. fmo–lcmo approach. J. Chem. Phys., 134(20):204109, 2011. URL: http://dx.doi.org/10.1063/1.3594100, arXiv:http://dx.doi.org/10.1063/1.3594100, doi:10.1063/1.3594100.

[RP14]

Pablo Ramos and Michele Pavanello. Quantifying environmental effects on the decay of hole transfer couplings in biosystems. J. Chem. Theory Comput., 10(6):2546–2556, 2014. URL: https://doi.org/10.1021/ct400921r, arXiv:https://doi.org/10.1021/ct400921r, doi:10.1021/ct400921r.